Modelling accounts receivable - alternative solution 1
What happens if the invoice payment lag is longer than the model timeline?
The way we model accounts receivable depends on the timeline of the model and the invoicing structure.
In the previous example, we had one customer, and the accounts receivable period was shorter than the timeline of the model. Therefore, some of the invoices would be paid within the model period, and some left unpaid to be received in the following period.
But often, we have to model other situations.
In this first Accounts receivable alternative, we will look at what happens if the accounts receivable period is longer than the model period.
In this example, we'll look at a situation where the model is monthly, with a two-month accounts receivable period.
This changes the way we need to model accounts receivable.
We are no longer looking at the "portion of revenue remaining unpaid" in the period.
Instead, we are thinking about this in terms of the length of the payment delay.
For this alternative solution, I have adapted our model so that the timeline is monthly. I've updated the revenue calculations accordingly.
The solution for this bonus material is available in the file pack you'll receive when you purchase the handbook. See file 4.53 FMH AR ALT1 END 01a.
Let's walk through how the Accounts receivable solution needs to change.
1. Monthly profile of the initial balance
We previously had an initial balance of accounts receivable that was all received on the "transaction date". Note - this date could also be the "last actuals date" in an operating model.
Given that the accounts receivable period is now longer than the model timeline, we now need to know the profile of when the opening balance will be received.
I've created an input section showing the monthly profile of the initial balance.
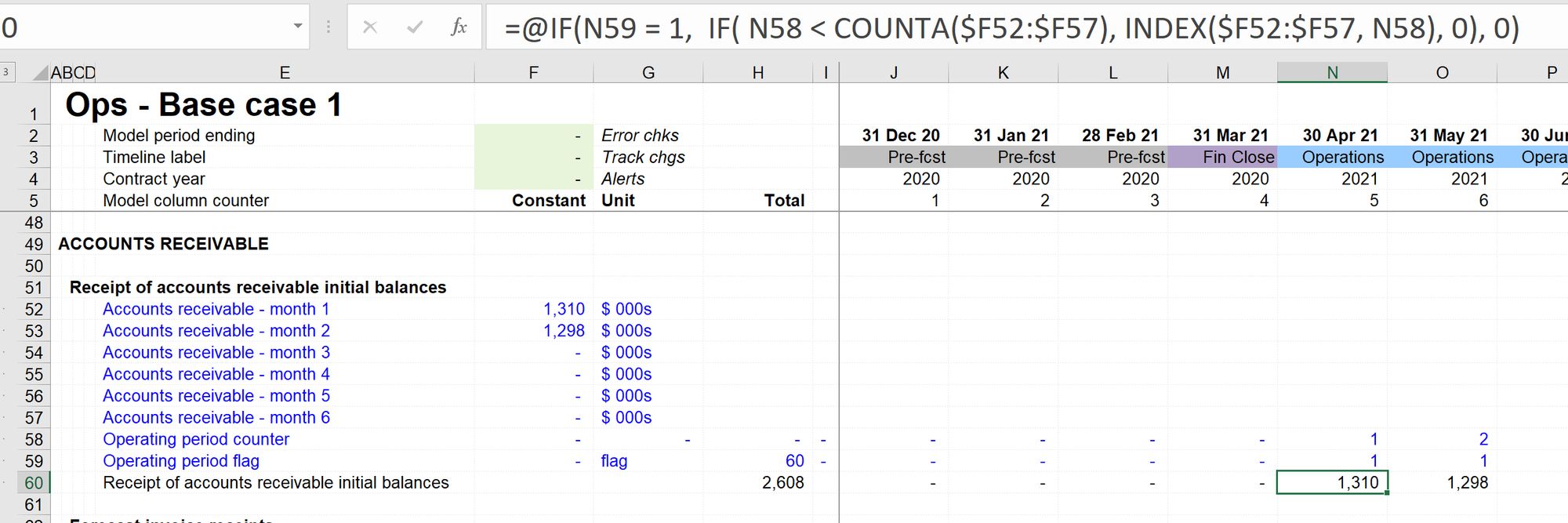
In this example, I've set up the calculation to have up to 6 months of initial accounts receivable balance profiled.
The calculation in row 60 is just about as long as I'd ever want to have in my model.
Here's the breakdown of what the different parts of the calculation are doing:
IF( N59 = 1 : This limits the calculation to only apply to the operating period.
IF( N58 < COUNTA($F52:$F57), : This limits the calculation to only apply to the first six operating periods. We could make the six an input. I've used the COUNTA function instead.
INDEX($F52:$F57, N58) : This uses the model column counter to "lookup" the correct accounts receivable balance and places it on the timeline in the correct month.
Another solution would be to use a series input for the initial accounts receivable balance.
2. Model the payment lag
The next block applies the two-month payment lag to revenue. There are multiple ways to achieve this in Excel. One common approach is to use OFFSET. As I've discussed elsewhere in this book, OFFSET is one of the "volatile functions" that we want to avoid wherever possible.
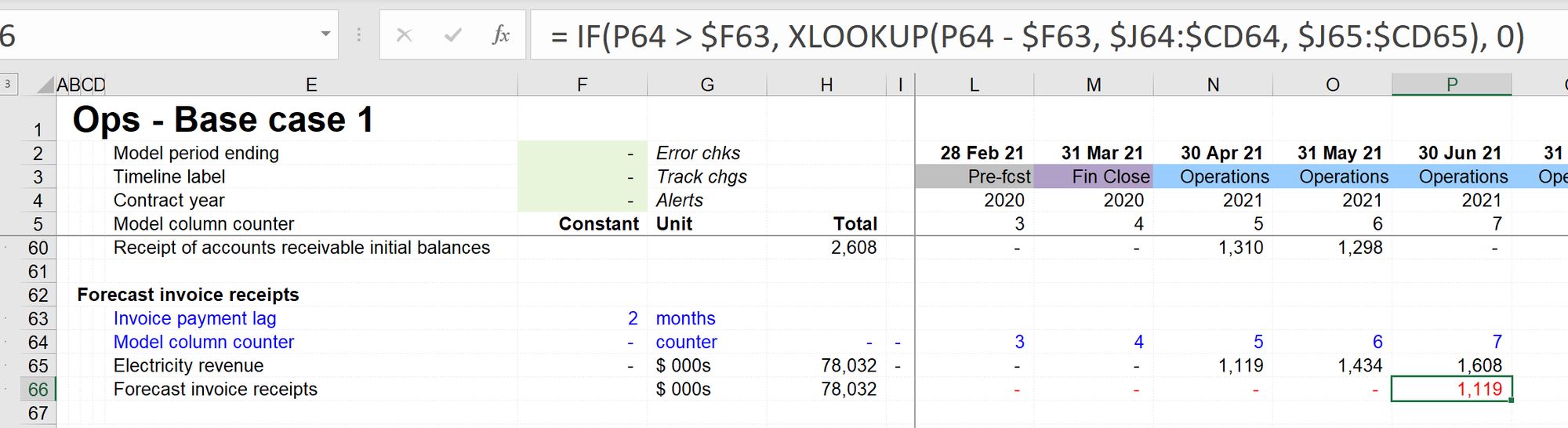
Instead, I'm using XLOOKUP. The XLOOKUP function has been used together with a model column counter. The function looks at the revenue line and returns the revenue from two periods ago by looking up the model column counter minus two. This allows us to change the length of payment delay dynamically without using an OFFSET set function.
As an early reader of this book pointed out, XLOOKUP requires you have the latest version of Excel. If you don't, there are other approaches you can use to achieve the same outcome.
Here's the same section modelled using SUMIF:
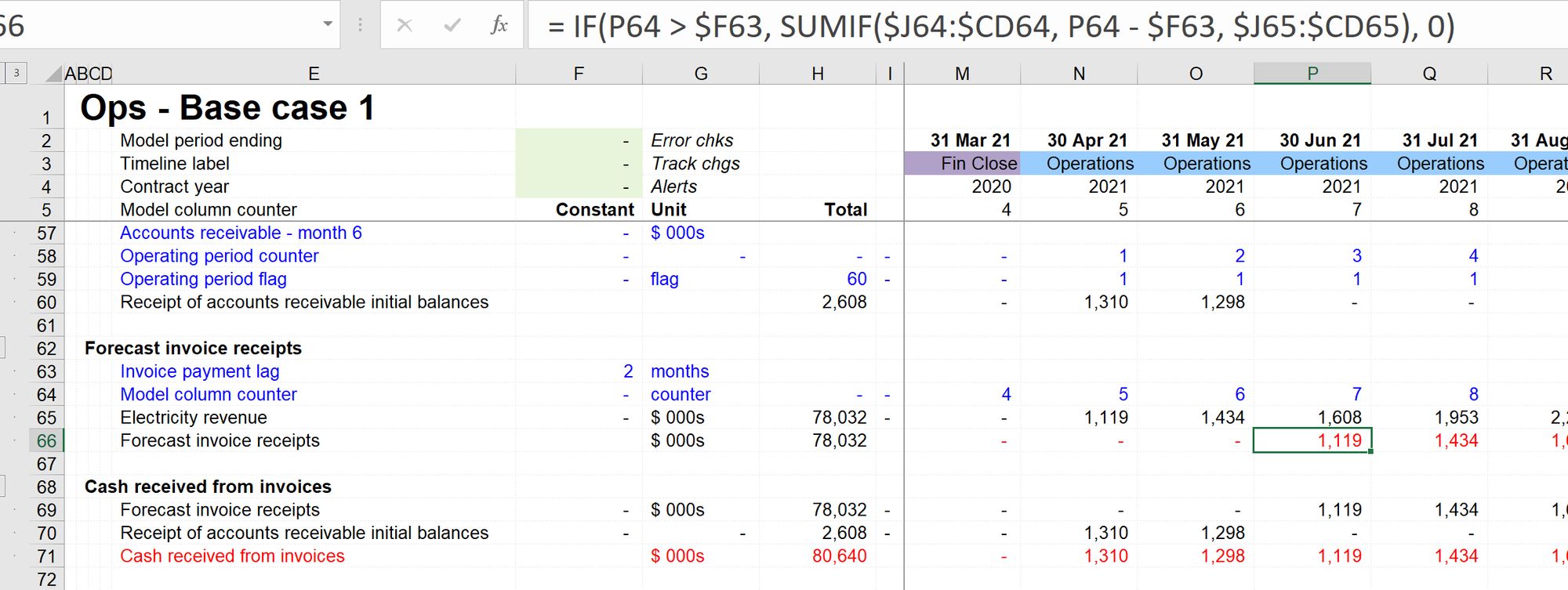
The solution file containing the SUMIF approach is available in the file pack you'll receive when you purchase the handbook. See file 4.53 FMH AR ALT1b END 01a.
In the final block, we add together the receipts of our initial balances in the first two months with our forecast of cash received from operation period invoices.
This line feeds the corkscrew and the cash flow as before
What if our invoices have different payment delays?
In this example, we apply one payment delay assumption to all our revenue.
It's common for businesses to have different payment delays for different products or customers.
We'll look at how this changes our calculation next.

Comments
Sign in or become a Financial Modelling Handbook member to join the conversation.
Just enter your email below to get a log in link.